عدد π یکی از مهم‌ترین ثابت‌های ریاضی است که در بسیاری از محاسبات علمی و مهندسی مورد استفاده قرار می‌گیرد. یکی از روش‌های تقریبی برای محاسبه‌ی مقدار π، روش مونت کارلو است که بر پایه‌ی اصول احتمالات و نمونه‌گیری تصادفی بنا شده است. در این مقاله، ابتدا به توضیح روش مونت کارلو پرداخته و سپس با ارائه‌ی یک پیاده‌سازی در زبان پایتون، مقدار تقریبی π را محاسبه می‌کنیم.

 

عدد π چیست؟

 

عدد π به عنوان نسبت محیط دایره به قطر آن، یکی از مهم‌ترین و پرکاربردترین اعداد در ریاضیات محسوب می‌شود. این عدد گنگ و متعالی است، به این معنی که نمی‌توان آن را به صورت یک کسر ساده نمایش داد و همچنین ریشه‌ی هیچ معادله‌ی چندجمله‌ای با ضرایب صحیح نیست. مقدار تقریبی π برابر با ۳.۱۴۱۵۹ بوده و تاکنون میلیاردها رقم اعشار آن توسط رایانه‌ها محاسبه شده است. این عدد در شاخه‌های گوناگون ریاضیات، فیزیک، مهندسی، و حتی علوم کامپیوتر اهمیت ویژه‌ای دارد.

 

روش مونت کارلو (Monte Carlo Method)

 

«شبیه‌سازی» (Simulation) روشی است برای تولید داده‌هایی که از توزیع آماری یک پدیده واقعی پیروی می‌کنند. اگرچه ممکن است داده‌های شبیه‌سازی شده کاملاً با واقعیت هم‌خوانی نداشته باشند، اما زمانی که جمع‌آوری داده‌ها یا اطلاعات یک پدیده هزینه‌بر و زمان‌بر باشد، شبیه‌سازی تبدیل به یک روش کارآمد و به‌ویژه اقتصادی برای مطالعه این پدیده‌ها می‌شود. از طرفی، روش «مونت کارلو» (Monte Carlo) که برای تحلیل سیستم‌های فیزیکی و اقتصادی به‌کار می‌رود، از تکرار شبیه‌سازی‌ها برای بررسی رفتار یک پدیده بهره می‌برد. 

 

روش مونته کارلو (Monte Carlo) یک تکنیک محاسباتی مبتنی بر شبیه‌سازی تصادفی است که برای حل مسائل پیچیده ریاضی، فیزیک، مهندسی، مالی، هوش مصنوعی و بسیاری از حوزه‌های دیگر استفاده می‌شود. این روش به‌ویژه زمانی کاربرد دارد که یک مسئله تحلیلی حل‌ناپذیر یا محاسبه‌پذیر اما بسیار دشوار باشد.

 

ایده‌ی اصلی این روش این است که به جای حل مستقیم یک مسئله، آن را به‌صورت یک فرآیند تصادفی مدل‌سازی کرده و با انجام تعداد زیادی شبیه‌سازی، یک تخمین عددی از پاسخ واقعی به‌دست آوریم. این روش معمولاً بر اساس نمونه‌گیری تصادفی از یک فضای ورودی و سپس تجزیه‌و‌تحلیل آماری این نمونه‌ها عمل می‌کند.

 

نام این روش از شهر مونته کارلو در موناکو گرفته شده است که به دلیل وجود کازینوها و بازی‌های شانسی معروف است. دلیل این نام‌گذاری این است که روش مونته کارلو نیز به اعداد تصادفی و احتمالات وابسته است، همان‌طور که قمار و شرط‌بندی به احتمال و شانس وابسته‌اند.

 

روش مونته کارلو به‌طور کلی شامل مراحل زیر است:

 

تعریف مسئله و مدل‌سازی آن: ابتدا باید مسئله را به شکلی فرمول‌بندی کنیم که بتوان آن را به‌صورت یک فرآیند تصادفی مدل کرد.

 

ایجاد نمونه‌های تصادفی: از توزیع‌های احتمالی مناسب، اعداد تصادفی تولید می‌شود که نشان‌دهنده‌ی داده‌های ورودی مسئله هستند.

 

اجرای شبیه‌سازی: محاسبات لازم بر روی نمونه‌های تصادفی انجام می‌شود و نتایج ثبت می‌گردد.

 

تحلیل و استخراج نتایج: پس از انجام تعداد زیادی شبیه‌سازی، میانگین یا سایر تحلیل‌های آماری بر روی نتایج انجام می‌شود تا تخمینی از پاسخ مسئله به‌دست آید.

 

اعتبارسنجی و کاهش خطا: با افزایش تعداد شبیه‌سازی‌ها، دقت تخمین بیشتر می‌شود. همچنین می‌توان از تکنیک‌هایی مانند نمونه‌گیری هوشمندانه برای بهبود کارایی استفاده کرد.

 

روش‌های محاسبه‌ی π

 

در طول تاریخ، دانشمندان و ریاضیدانان بسیاری تلاش کرده‌اند تا مقدار π را با دقت بیشتری محاسبه کنند. از جمله روش‌های معروف برای این کار می‌توان به موارد زیر اشاره کرد:

 

1. روش ارشمیدس: ارشمیدس، ریاضیدان یونانی، از چندضلعی‌های محاطی و محیطی برای تقریب مقدار π استفاده کرد. او نشان داد که مقدار π بین ۳.۱۴۰۸ و ۳.۱۴۲۸ قرار دارد.

 

2. روش سری‌های نامتناهی: یکی از معروف‌ترین سری‌هایی که برای محاسبه‌ی π به کار می‌رود، سری گرگوری-لایب‌نیتس است:. این سری همگرا است، اما به کندی، و برای دستیابی به دقت بالا، به تعداد زیادی جمله نیاز دارد.

 

3. روش مونت کارلو: این روش مبتنی بر شبیه‌سازی تصادفی است و با استفاده از اصول احتمالات، مقدار تقریبی π را محاسبه می‌کند. برای اجرای این روش، نقاطی به طور تصادفی در یک مربع واحد در نظر گرفته می‌شوند و بررسی می‌شود که چه تعداد از این نقاط درون یک ربع دایره قرار می‌گیرند. با توجه به نسبت تعداد نقاط درون دایره به کل نقاط، می‌توان مقدار تقریبی π را تخمین زد.

 

4. روش گاوس-لژاندر: این روش عددی بسیار سریعی برای محاسبه‌ی π است و همگرایی بالایی دارد. این روش مبتنی بر میانگین حسابی-هندسی دو عدد و یک دنباله‌ی کمکی است.

 

5. الگوریتم‌های رایانه‌ای مدرن: امروزه، با استفاده از الگوریتم‌های پیچیده‌ای همچون الگوریتم‌های FFT (تبدیل فوریه سریع) و روش‌های عددی پیشرفته، مقدار π تا تریلیون‌ها رقم اعشار محاسبه شده است.

 

محاسبه عدد پی با استفاده از روش مونت کارلو (Monte Carlo Method) 

 

برای درک بهتر این روش، بهتر است تفاوت آن با شبیه‌سازی را با یک مثال توضیح دهیم. 

 

شبیه‌سازی نتایج بازی شیر یا خط: ابتدا یک متغیر تصادفی با توزیع یکنواخت در بازه (0,1) تولید می‌کنیم. اگر این مقدار بیشتر از ۰.۵ باشد، نتیجه شیر است و در غیر این صورت خط خواهد بود. اینگونه بازی شیر یا خط شبیه‌سازی می‌شود.

 

روش مونت کارلو: هزار عدد تصادفی از توزیع یکنواخت در بازه (0,1) تولید می‌کنیم. تعداد اعداد بیشتر از 0.5 نشان‌دهنده شیرها و آن‌هایی که کمتر از 0.5 هستند، تعداد خط‌ها را نشان می‌دهند. بنابراین با تکرار این شبیه‌سازی می‌توانیم در مورد عدم تعادل سکه قضاوت کنیم. اگر نسبت شیرها به خط‌ها نزدیک به ۱ باشد، سکه را متعادل می‌دانیم.

 

هر چه تعداد تکرارها در شبیه‌سازی‌های روش مونت کارلو بیشتر باشد، نتایج به دست آمده قابل اعتمادتر خواهند بود. ویژگی خاص روش مونت کارلو، توانایی حفظ داده‌های مفید و حذف داده‌های نامناسب است که به تکنیک «قبول-رد» (Accept-Reject) معروف است.

 

یکی از مشهورترین کاربردهای روش مونت کارلو، محاسبه عدد «پی» (π) است که در محاسبه محیط یا مساحت دایره به کار می‌رود. البته روش‌های دیگری نیز برای محاسبه عدد پی وجود دارد، از جمله شیوه سوزن بوفون. برای محاسبه این عدد باید نسبت مساحت دایره به مربع شعاع آن را یافت.

 

π = area / radius²

 

اگر شعاع دایره را ۱ در نظر بگیریم، مساحت دایره برابر با عدد پی خواهد شد. حال یک مربع با ضلع ۲ در نظر می‌گیریم که دایره با شعاع ۱ درون آن قرار دارد. در اینجا، دو متغیر تصادفی مستقل از توزیع یکنواخت در بازه (-1, 1) تولید می‌کنیم که آن‌ها را x و y می‌نامیم. بنابراین نقاط (x,y) درون مربع قرار می‌گیرند. مساحت مربع برابر با ۴ است.

 

نقاط داخل دایره باید رابطه x² + y² ≤ 1 را رعایت کنند که این نقاط را قبول می‌نامیم. سایر نقاط را که این رابطه را ندارند، رد می‌کنیم. نسبت تعداد نقاط داخل دایره (مساحت دایره) به تعداد کل نقاط تولید شده (مساحت مربع) برابر با یک چهارم عدد پی است. بنابراین با ضرب این نسبت در ۴ می‌توانیم عدد پی را محاسبه کنیم.

 

 

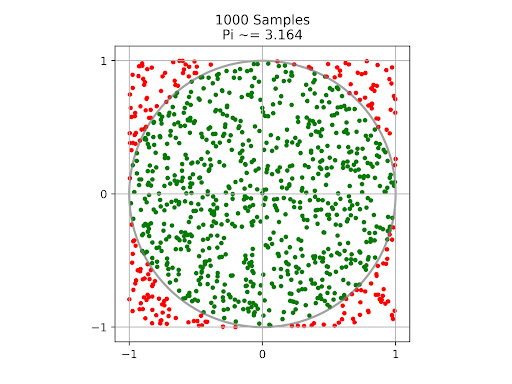
روند حل مسئله در روش مونت کارلو

 

روند حل مسئله در روش مونت کارلو روش مونت کارلو معمولاً مراحل زیر را در بر می‌گیرد، اگرچه ممکن است در بعضی موارد تفاوت‌هایی وجود داشته باشد:

1. ویژگی‌های داده‌های ورودی تعیین می‌شوند (مثلاً بازه -1 تا 1 برای تولید اعداد تصادفی به منظور محاسبه عدد پی).
2. داده‌های تصادفی ورودی تولید می‌شوند (انتخاب توزیع یکنواخت برای تولید اعداد تصادفی جهت محاسبه عدد پی).
3. محاسبات روی داده‌های تصادفی انجام می‌شود (محاسبه روابط مربوط به دایره).
4. نقاط قبول و رد در نتیجه شبیه‌سازی تعیین می‌شوند (نقاط داخل دایره پذیرفته می‌شوند و نقاط بیرون دایره رد می‌شوند).
5. محاسبات نهایی انجام می‌شود تا پاسخ پرسش اصلی به دست آید (محاسبه ۴ برابر نسبت مساحت دایره به مربع).